

The string notation and the bold symbols are defined in the text. (a) P / O +-type portrait (b) O +-type portrait (c) P / O 2-type portrait. Unit-disk representation of phase portraits for spin-torque-driven magnetization dynamics, with examples of limit cycles present in one or more energy regions as a result of the injection of the spin-polarized current. One can create a direct correspondence between these conservative phase portraits and the spin-torque portraits for the same field value and α ≠ 0, β ≠ 0, by using the following facts:įIGURE 9.2.

Region H has also disappeared and only two energy extrema at m x = ± 1 are present.
This phase portrait is realized for | a x | ≥ 1, i.e., | h a x | ≥ D z − D x. The symbol d − ( d +) expresses the fact that the fixed point m x = − 1 ( m x = 1) is now a saddle. One of the low-energy regions, e.g., region L − under positive field, has disappeared. These are the phase portraits existing for k ′ 2 ≤ | a x | ≤ 1, i.e., D y − D x ≤ | h a x | ≤ D z − D x. According to Figs 4.5 and 4.10 Fig. 4.5 Fig. 4.10, there are three distinct phase portraits for this field direction: These portraits have been extensively analyzed in Chapter 4.
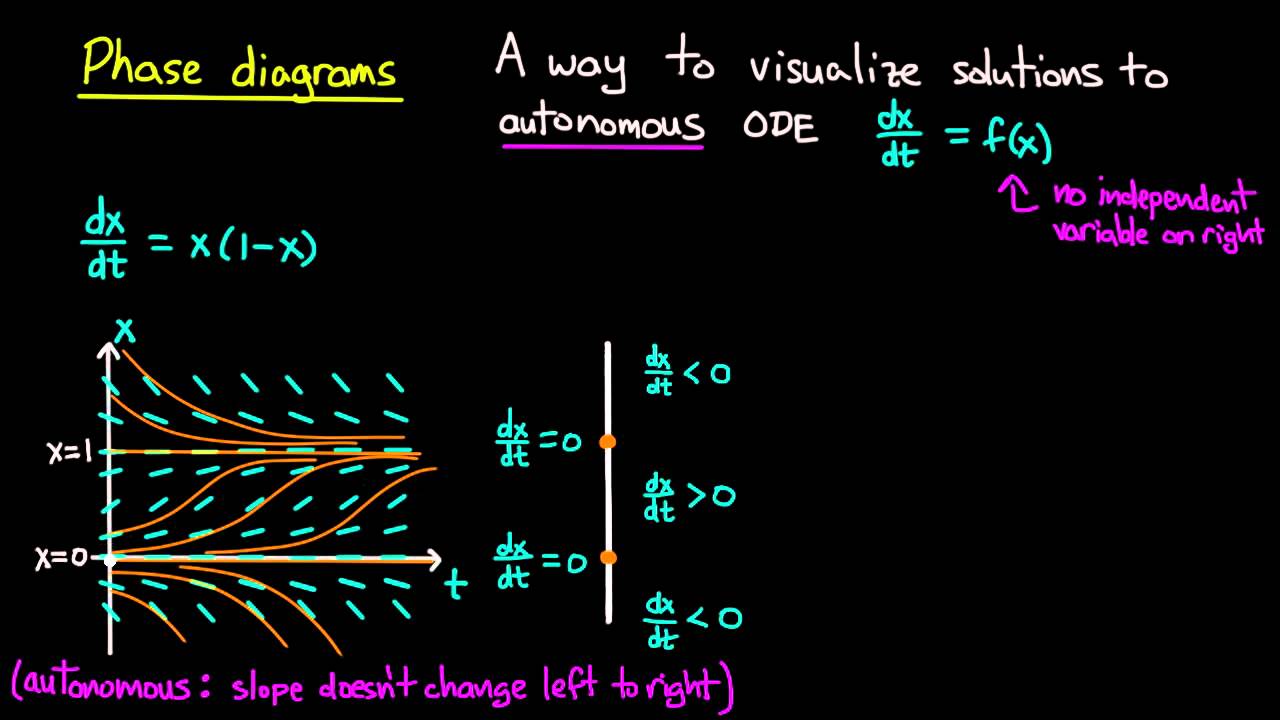
#Hot to draw phase planes for differential equation systems free
The phase portraits of interest here are those that correspond to the field aligned along the easy axis of the free layer, i.e., the x axis. In order to demonstrate how this can be accomplished, let us first recall that all the essential information about a generic conservative portrait can be coded by listing the number of saddles, central regions, and fixed points present in this portrait. Therefore, one expects that the classification of conservative phase portraits discussed in Chapter 4 can be instrumental in the description of spin-transfer effects as well. This fact implies that the phase portraits of the dynamics can be viewed as perturbations of the corresponding conservative phase portraits obtained for the same value of the field and α = β = 0. It has been previously mentioned that an essential role in the analysis of spin-transfer-driven magnetization dynamics is played by the fact that α and β are small quantities, of the order of 10 −2 or less. The final result of this study will be the theoretical stability diagram shown in Figs 9.3 and 9.4. The knowledge of the location and nature of these lines is essential for the interpretation of spin-transfer experiments. These bifurcation conditions result in bifurcation lines in the ( h a x, β / α )-plane. However, there exist bifurcation conditions where the control-parameter change leads to qualitative changes in the phase portrait, namely changes in the number and stability of fixed points and limit cycles.

When a small change in the control parameters induces correspondingly small, continuous modifications in the phase portrait, the portrait is said to be structurally stable. For each point in the ( h a x, β / α ) control plane, we shall determine the corresponding phase portrait for the magnetization dynamics and follow the evolution of this portrait as the field or the current is varied. The parameter β / α will be used to represent the current density. Claudio Serpico, in Nonlinear Magnetization Dynamics in Nanosystems, 2009 9.4 Phase Portraits and Bifurcationsīased on the discussion presented in the previous sections, we shall now determine the stable stationary states as well as the steady-state self-oscillations present in a spin-transfer device subject to the external field h a x along the free-layer easy axis and the spin-polarized current density J e.


 0 kommentar(er)
0 kommentar(er)
